Elaborazione digitale di
immagini
Argomenti trattati:
1-Immagini digitali
1.1-Immagini create
dai numeri primi: la spirale di Ulam
2-Manipolazioni
dei pixel
2.1-
Insiemi di Julia e bacini di attrazione
3-Manipolazioni
geometriche
3.1-Manipolazioni geometriche con
funzioni di variabile complessa
4-Decomposizione
spettrale, filtraggio e compressione
5-Restauro
di immagini degradate
6-Crittografia
con le immagini
1-Immagini digitali
Un'immagine digitale in bianco nero può essere descritta da
una matrice m×n
di pixel (contrazione di picture element). Il generico pixel
p(i,j), il cui valore numerico può essere intero o
reale, fornisce la luminosità del punto di coordinate (i,j)
dell'immagine.
Formato PGM (Portable Gray
Map). Nella convenzione PGM il file che contiene le informazioni
sull'immagine è organizzato nel modo seguente:
P2
# eventuali commenti
numero_colonne, numero_righe
valore_livello_bianco
p(1,1)
p(1,2)
.
.
p(1,n)
p(2,1)
p(2,2)
.
.
dove:
P2 indica al sistema
che visualizzerà il file sullo schermo
che si tratta di una immagine bianco nero nel formato PGM
#
eventuali commenti sono commenti arbitrari preceduti
da #
numero_colonne e
numero_righe sono due
interi che determinano le dimensioni dell'immagine (matrice dei
pixels)
valore_livello_bianco
è un intero che determina il valore numerico del bianco
(generalmente 255), mentre il valore numerico del nero è 0.
p(i,j) sono i valori numerici
dei pixels (fra 0 e valore_livello_bianco) relativi alla posizione
(i,j). Essi sono ordinati per righe.
Maggiori informazioni si trovano nel sito netpbm.sourceforge.net
Esistono diversi programmi per visualizzare un'immagine sullo
schermo di un computer. Due pacchetti che girano sotto linux sono xv
e gimp.
Ad esempio, se
immagine.pgm è il nome di un file che contiene un'immagine
codificata nel formato PGM, allora il comando
xv immagine.pgm
visualizza sullo schermo il contenuto di immagine.pgm.
Esempio di file PGM
P2
# esempio semplice
4,4
255
0
0
0
0
0
255
255
0
0
255
255
0
0
0
0
0
La stessa immagine poteva essere memorizzata come
P2
#
esempio semplice
4,4
255
0 0
0 0
0 255 255 0
0 255 255 0
0
0 0 0
File ASCII e file RAW
Un file PGM puό essere
memorizzato nella modalità ASCII o nella modalità RAW.
Nella modalità ASCII il valore del generico pixel viene
scritto nella sua rappresentazione decimale con caratteri ASCII. Ad
esempio. se il valore del pixel è 123, vengono scritte le tre
cifre 1,2 e 3, consumando quindi tre byte di memoria, uno per
ciascuna cifra, più altri tre byte per gli spazi di
separazione. Nella rappresentazione RAW, il pixel il cui valore è
123 viene memorizzato con il singolo byte il cui valore è 123.
In questo modo un solo byte è sufficiente per ciascun pixel.
Nella rappresentazione RAW la stringa P2 va sostituita con P5. La
rappresentazione ASCII è più comoda perché
permette di essere visualizzata e manipolata più facilmente.
Ha lo svantaggio che è più ingombrante. Noi useremo la
rappresentazione ASCII.
Per semplicità eviteremo di scrivere commenti nei file PGM.
L'applicazione Gimp di Linux permette di aprire un file
immagine in un qualsiasi formato e salvarla in un altro
formato diverso. Ad esempio, una fotografia digitale salvata come
file jpeg puό essere aperta da Gimp e salvata come file PGM.
Il linguaggio di programmazione Octave permette in modo semplice
di trasformare una matrice di numeri in una immagine usando la stessa
logica dello standard pgm. Se ad esempio la variabile A
contiene una matrice di m righe e n colonne con valori
numerici A(i,j), il comando
imshow(A, [nero,bianco]);
mostra sullo schermo una immagine formata da m×n
pixel dove la luminosità del pixel di posizione (i,j) è
data da A(i,j) e dove l'intervallo della scala dei
grigi è [nero, bianco], cioe il valore numerico di nero
corrisponde al nero mentre il valore numerico di bianco
corrisponde al bianco. Ponendo il vettore vuoto [ ] al posto di
[nero,bianco] i valori di nero e di bianco vengono presi uguali al
minimo e al massimo dei valori di A. La sintassi del comando di
imshow puό essere diversa a seconda della versione di Octave.
Esempio 1. Il programma Octave seguente costruisce
un'immagine n×n
con valori di grigio che sfumano da nero a bianco secondo la regola
A(i,j)=i+j, e dove 2 corrisponde a nero e 2n
a bianco.
function grigi (n)
a=zeros(n);
for i=1:n
for j=1:n
a(i,j)=i+j;
end
end
imshow(a);
end
L'immagine che si ottiene in questo modo è la seguente:

se poi vogliamo creare un file che contiene i dati di questa
immagine nel formato pgm basta inserire nella function precedente i
seguenti comandi:
fid=fopen('grigi.pgm', 'w');
fprintf(fid,
'P2\n');
fprintf(fid, '%d , %d \n' , n , n);
fprintf(fid, '255\n');
for i=1:n
for j=1:n
fprintf(fid, '%d\n', a(i,j) );
end
end
Il comando fopen di
Octave apre un file per la lettura/scrittura la sintassi è
fid=fopen(nomefile, modo) dove
nomefile è
una stringa col nome del file che si vuole aprire, modo
è una stringa che contiene la modalità di apertura, in
particolare:
'w' write (file di
scrittura)
'r' read (file di
lettura)
la variabile fid
prende come valore un numero intero che servirà a identificare
il file di lettura/scrittura. Infatti, l'istruzione
fprintf(fid, 'scrivo %d',n);
scrive il valore intero della variabile n
preceduto dalla parola scrivo. La
sintassi per i formati di scrittura è la stessa del linguaggio
C.
2.1-Immagini
create dai numeri primi: la spirale di Ulam
Immagini interessanti possono essere
costruite per evidenziare proprietà dei numeri primi
Esempio 2. Costruiamo una immagine n×n
tale che il pixel di posto (i,j) sia bianco se n(i-1)+j
è un numero primo, sia nero altrimenti. Per questo ci occorre
una funzione che dato un intero p ci dice se p è
primo o no.
function evidenzia_primi
(n)
imag=zeros(n);
for
i=1:n
for
j=1:n
if
(primo(n*(i-1)+j))
imag(i,j)=1;
end
end
end
imshow(imag);
end
function v=primo(p)
v=1;
for
i=2:sqrt(p)
if(mod(p,i)==0)
v=0;
break;
end
end
end
La figura che si ottiene con n=100 è
la seguente

Un pochino più complicato, ma vale
la pena farlo, è numerare i pixel lungo una spirale che si
dipana dal centro del quadrato, partendo dal numero 1

e accendere i pixel che corrispondono ai
numeri primi. In questo modo si ottiene la spirale
di Ulam.

Un programma che la genera è il seguente
function spirale_di_ulam
(n)
centro=n;
n=2*n+1;
a=zeros(n);
lato=0;
p=1;
i=centro;
j=centro;
giri=centro-1;
% traccia i quattro lati della spirale
for
k=1 : giri
% tratto sud:
movimento orizzontale a destra
lato=lato+1;
for
ell=1 : lato
p=p+1;
j=j+1;
a(i,j)=primo(p);
end
% tratto est: movimento verticale in
alto
for
ell=1 : lato
p=p+1
;
i=i-1
;
a(i,j)=primo(p)
;
end
% tratto nord: movimento orizzontale a
sinistra
lato=lato+1
;
for
ell=1 : lato
p=p+1;
j=j-1;
a(i,j)=primo(p);
end
% tratto ovest: movimento
verticale in basso
for
ell=1 : lato
p=p+1;
i=i+1;
a(i,j)=primo(p);
end
end
% scrivi
spirale
fid=fopen('ulam.pgm',
'w');
fprintf(fid,
'P2\n');
fprintf(fid,
'%d %d \n', n,n);
fprintf(fid,
'255\n');
for
i=1 : n
for
j=1 : n
fprintf(fid,
'%d\n', a(i,j)*255);
end
end
fclose(fid);
end
Abbiamo spezzato la numerazione degli interi lungo la spirale in
quattro parti, ciascuna per ciascun lato della spirale. Infatti la
variabile k conta i giri della
spirale intorno al suo centro, e per ciascun giro si percorrono i
quattro lati.
Il linguaggio Octave, essendo interpretato, ha tempi di
elaborazione molto elevati. In particolar modo questo succede in
presenza di cicli for annidati. Usando Octave siamo in grado di
trattare dimensioni relativamente basse e quindi immagini piccole.
Per poter svolgere elaborazioni a dimensione più ampia occorre
implementare gli algoritmi con linguaggi più efficienti tipo
il linguaggio C o il Fortran 90. Una alternativa accettabile è
usare Matlab che usa la stessa sintassi di Octave ma che è
molto più efficiente, oltre che ad essere un prodotto
commerciale.
Provate a evidenziare le coppie di numeri interi (p,q)
tali che p*p+q*q è un numero primo. Per questo create
una immagine di dimensione (2m+1)×(2m+1),
dove m è un intero assegnato ad esempio m=100, e
accendete il pixel in posizione (i,j) se
(i-m)*(i-m)+(j-m)*(j-m) è un
numero primo. Provate a creare immagini analoghe con condizioni
diverse del tipo |p*p-q*q|+k è primo per un
fissato k=1,2,3; oppure p*p+q*q+k è primo per un
fissato k=1,2,3; oppure p*p+q*q+k è primo sia
per k=1 che per k=3; o, ancora p*q+1 è
primo. In quest'ultimo caso si ottiene

Guardando attentamente questa immagine si riescono a evidenziare
particolari forme geometriche.
Provate a evidenziare le coppie (p,q) di numeri primi
consecutivi (primi gemelli).
2-Manipolazione dei pixel
Esempio 3. Vediamo come è possibile trasformare
un'immagine in negativo. Supponiamo di avere nel file foto.pgm una
fotografia che vogliamo leggere, trasformare in negativo e
registrarla in un file diverso. La trasformazione che dobbiamo
applicare a ciascun pixel è f(p)=255-p
function negativo(nome_file)
fidr=fopen(nome_file,
'r'); % aprefile
di lettura
fidw=fopen('negativo.pgm',
'w'); % apre
file di scrittura
ch=fscanf(fidr,
'%s', '1'); % legge
numero magico come stringa
fprintf(fidw,
'%s\n', ch); % scrive
numero magico come stringa
n=fscanf(fidr,
'%d', '1'); % legge
numero colonne come intero
m=fscanf(fidr,
'%d', '1'); % legge
numero righe come intero
fprintf(fidw,
'%d %d\n', [ n m]); % scrive
numero di righe e di colonne
liv=fscanf(fidr,
'%d', '1'); % legge
numero di livelli
fprintf(fidw,
'%d\n', liv); % scrive
numero di livelli
for
i=1:m
for
j=1:n
pix=fscanf(fidr,
'%d', '1'); % legge
valore pixel (i,j)
fprintf(fidw,'%d\n',
255-pix); % scrive
in negativo il valore del pixel (i,j)
end
end
end
Esempio 4. Cosa succede dell'immagine se applichiamo la
trasformazione f(p)=min(255,p+20) oppure f(p)=max(0,p-20). Cosa
succede invece se la trasformazione è f(p)=min(255, 2p) oppure
f(p)=parte_intera(p/3)? Osservate che le operazioni di min e max
servono a tenere il valore della funzione dentro il segmento
consentito [0,255]. Osservate ancora che occorre prendere la parte
intera. Mediante queste trasformazioni si cambiano globalmente la
luminosità e il contrasto di una immagine. Volendo, potete
aumentare il contrasto e schiarire le zone scure lasciando la
situazione inalterata nelle zone chiare, ad esempio con
f(p)=p se p>128
f(p)=max(2p,128) se p<=128
Ancora provate a portare in negativo solo le zone buie
dell'immagine con
f(p)=255-p se p<=128
f(p)=p se p>128.
Ecco cosa si ottiene a partire dalla seguente immagine a colori

se usiamo come soglia p=50 (per come si codificano le immagini a
colori si rimanda al successivo punto)

Immagini a colori, modalità
RGB
Una immagine a colori può essere memorizzata mediante la
modalità RGB (Red, Green, Blue). In questo modo ad ogni pixel
viene assegnata una terna di numeri r,g,b, dove r fornisce
l'intensità del rosso, g l'intensità del verde e b
l'intensità del blu. Il file che viene costruito nel formato
PPM (Portable Pixel Map) è organizzato come segue
P3
# eventuali commenti
numero_colonne, numero_righe
massima_luminosità
r(1,1) g(1,1)
b(1,1)
r(1,2) g(1,2) b(1,2)
.
.
.
Ciò che cambia rispetto ad un file b/n è la prima
riga che contiene P3 a indicare che è un file a colori nella
modalità RGB e la presenza delle terne di pixel (un valore per
ogni colore) anziché dei singoli valori. Le terne dei valori
rgb possono non stare sulla stessa riga ma essere distribuite su
righe consecutive. Nella codifica RAW la stringa P3 viene sostituita
da P6.
Maggior dettagli si trovano a
netpbm.sourceforge.net
Il formato PNM, acronimo di Portable Any Map, è giusto
un'astrazione dei formati PBM, PGM, and PPM. Cioè il termine
PNM si riferisce collettivamente a PBM, PGM, e PPM.
Usando octave, dopo aver creato le tre matrici R,G,B che danno la
luminosità delle componenti di rosso, verde e blu, per
mostrare l'immagine a colori corrispondente basta digitare
imshow(R,G,B,[ ]); oppure a seconda della versione di octave,
imshow(H,[ ]); dove H è una matrice a tre indici tale che
H(:,:,1)=R; H(:,:,2)=G, H(:,:,3)=B;
Potete provare a effettuare le manipolazioni di contrasto e
luminosità sui singoli colori in modo diverso da colore a
colore, oppure potete scambiare il rosso col blu o portare solo il
verde in negativo o mescolare i colori su ciascun pixel secondo una
regola prefissata, ad esempio, r'=3r+g-2b
mod 256, g'=r+2g+b mod 256, b'=r-g+b
mod 256 e vedere l'effetto sull'immagine.
Come è possibile
trasformare un'immagine da colori a b/n?
Nella foto che trovate
qui di seguito provate a modificare solamente la componente g
del verde di ogni pixel (lasciando rosso e blu inalterati) nel
seguente modo: se il valore g del pixel è minore o
uguale a 200 sostituite g con 200-g altrimenti lasciate
g inalterato. L'effetto è quello di mettere in negativo
solo alcuni livelli di luminosità del verde.
Immagine originale

Immagine modificata

2.1- Insiemi di Julia e
bacini di attrazione
Esempio 5. (Insiemi di Julia e bacini di attrazione).
Sapreste costruire un'immagine che rappresenti i bacini di attrazione
del metodo di Newton per risolvere equazioni del tipo z^n-1=0? Ad
esempio:


Considerate il metodo di Newton applicato all'equazione z3-1=0
che genera la successione definita da
zk+1=zk-(zk3-1)/(3zk2),
a partire da z0. Create una immagine nel
seguente modo: per p intero ponete h=1/p e considerate
una griglia di (2p+1)×(2p+1)
punti zi,j nel quadrato [-1,1]×[-1,1]
del piano complesso definiti da wi,j=jh+Iih,
i=-p,p, j=-p,p, dove I
denota l'unità immaginaria tale che I2=-1.
Associate ad ogni zi,j un pixel di una immagine
(2p+1)×(2p+1).
Posto z0=wi,j considerate
la successione zk generata dal metodo di
Newton e colorate rispettivamente di rosso verde e blu il pixel che
corrisponde al punto wi,j se la successione
zk converge a 1, -1/2+i*sqrt(3)/2,
-1/2-i*sqrt(3)/2. Come test di convergenza usate la condizione |zk
-zk+1| minore di 1/10000.
Fate
un analogo disegno dando ai tre colori una intensità diversa a
seconda del numero k di iterazioni richieste perché sia
soddisfatto il test di convergenza.
Provate a dare ancora una
colorazione diversa assegnando la quantità r,g,b di rosso,
verde e blu in funzione del numero di iterazioni mediante tre
funzioni diverse, ad esempio r=1231k mod 256, g=2753k
mod 256, b=3127k mod 256.
Provate a tracciare
disegni analoghi per il metodo di Newton applicato alle equazioni:
x2-x-1=0, x-x-2=0 e 1-x-3=0
e confrontate i disegni cosi' ottenuti.
Modificate il programma
in modo che anziché il quadrato [-1,1]×[-1,1]
viene considerato il quadrato di centro (x0,y0)
e semilato s.
Ecco alcune immagini cosi' ottenute
Equazione x3-1=0

Equazione x2-x-1=0

Equazione x-x-2=0

Equazione 1-x-3=0

È possibile creare dei filmati
come il seguente che traccia i bacini di attrazione del metodo di
Newton applicato all'equazione x^p-1=0 con p che varia tra 3 e 4. Il
filmato è stato creato da uno studente del corso a.a.
2008-2009.
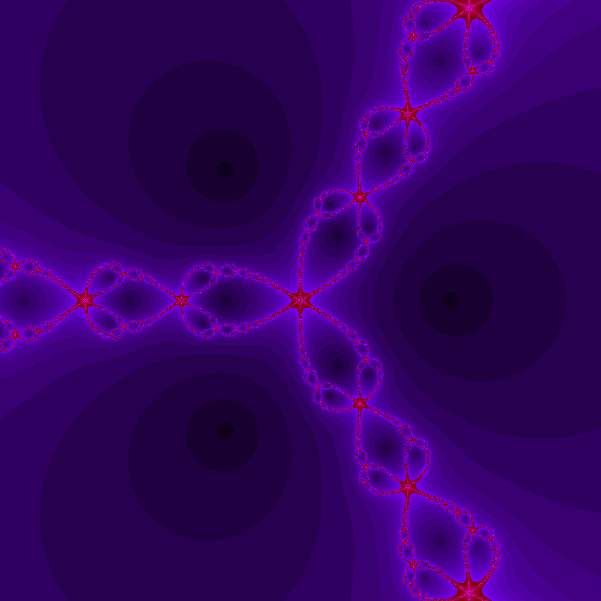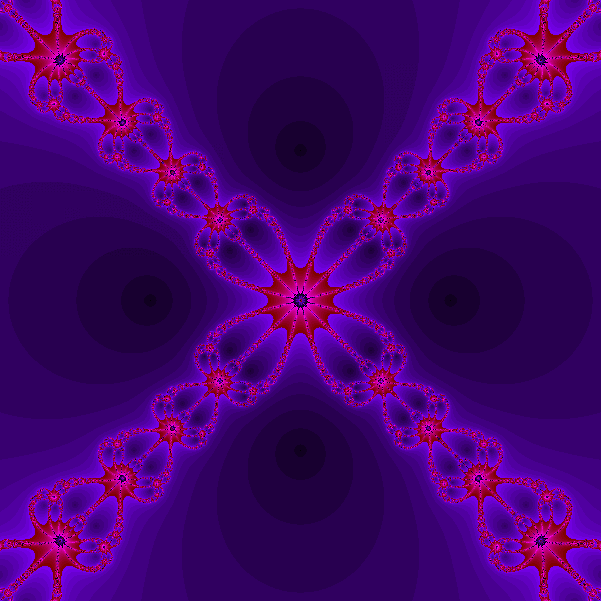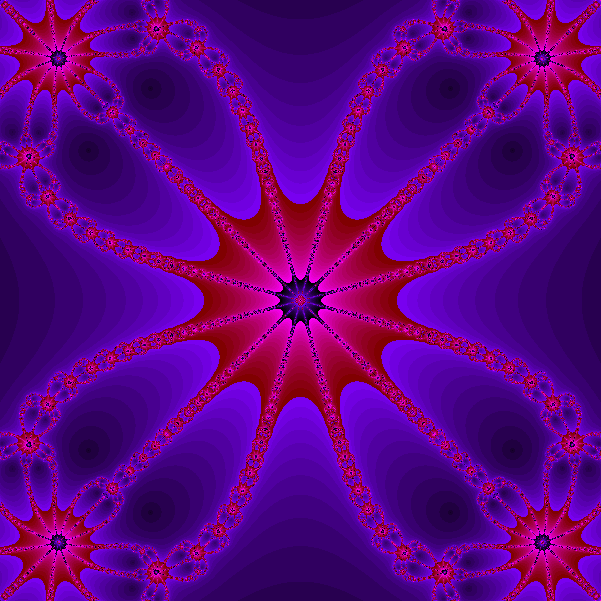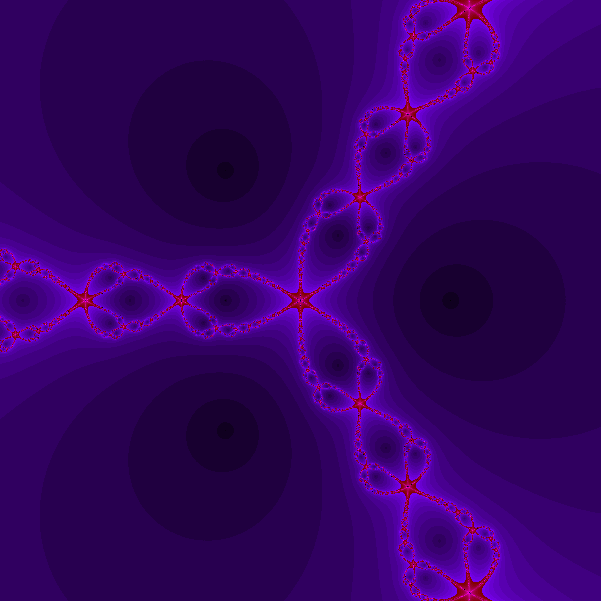
Esempio 6. Evidenziare i contorni. Sapreste trattare il
problema di evidenziare i contorni di una immagine assegnata? Provate
a generare le seguenti immagini


I contorni di una immagine sono i punti in cui la luminosità
ha una variazione brusca. Per evidenziarli sarebbe sufficiente creare
una nuova immagine con pixel uguali a 0 (nero) dove la luminosità
è costante o subisce piccole variazioni e con pixel 255
(bianco) nei punti in cui la luminosità ha forti variazioni.
Per una funzione da f:R→ R sufficientemente regolare la variazione
è espressa dalla sua derivata prima: intuitivamente |f'| è
piccola dove la f ha piccole variazioni è grande in
corrispondenza delle grandi variazioni di f. Anche la derivata
seconda f” è legata alle variazioni di f. Per una funzione
definita su un dominio discreto (1,2,3,...,n) la derivata prima viene
sostituita con la differenza prima che nel punto i vale
(f(i+1)-f(i-1))/2 e la derivata seconda con la differenza seconda che
nel punto i vale f(i-1)-2f(i)+f(i+1). Nel caso di funzioni di due
variabili x,y, come accade per le immagini possiamo considerare come
indice di salto la somma delle derivate parziali rispetto alla x e
rispetto alla y, oppure il laplaciano cioè la somma delle
derivate seconde rispetto alla x e rispetto alla y. Nel caso discreto
abbiamo rispettivamente (f(i+1,j)-f(i-1,j) +f(i,j+1)-f(i,j-1))/2
e f(i-1,j)+f(i+1,j)+f(i,j-1)+f(i,j+1)-4f(i,j). Quest'ultima
espressione è detto laplaciano discreto. Provate a sostituire
l'immagine originale con quella ottenuta applicando il laplaciano
discreto a tutti i punti dell'immagine riaggiustando il fattore di
scala in modo da poter avere sia valori di bianco che valori dii
nero. Provate a costruire altri operatori discreti che siano
discretizzazioni di derivate di ordine più elevato.
Altri formati
La codifica di tipo PGM, anche nella modalità RAW ha lo
svantaggio di essere molto ingombrante. Esistono altri modi piu o
meno vantaggiosi di rappresentare file di immagini. Un formato
particolarmente usato, che però conduce ad un degrado
qualitativo dell'immagine è il formato JPG. Esso si basa su
tecniche di compressione ottenute mediante trasformate di coseni.
Vedremo più avanti cosa questo significhi.
3-Manipolazioni geometriche.
È possibile ruotare una immagine attorno al pixel di
coordinate (i0,j0) semplicemente applicando una
rotazione alle coordinate di ciascun pixel, cioè copiando nel
pixel di coordinate (i,j) il valore del pixel di coordinate (i',j')
per i=1,...,m, j=1,...,n, dove
i'=i0+[
(i-i0)*cos(a)+(j-j0)*sin(a)]
j'=j0+[(i-i0)*sin(a)-(j-j0)*cos(a)]
Il programma che realizza questa trasformazione è il
seguente
% ruota un'immagine attorno il pixel
(i0,j0)
function
rotazione(immagine, angolo)
%
apre
il file 'immagine' e legge l'immagine rgb nelle matrici r,g,b
%
apre
il file di output con identificatore fidw e scrive l'intestazione
..........
..........
% ruota l'immagine
attorno al centro
i0 = round(m/2);
a=angolo;
j0 = round(n/2);
for
i = 1 : m
for
j = 1 :
n %
seleziona
il pixel di posizione (i,j) dell'immagine ruotata
ip =
round(i0+(i-i0)*cos(a)+(j-j0)*sin(a)); %
calcola
il pixel di posizione (ip,jp) dell'immagine di provenienza
jp = round(j0+(i-i0)*sin(a)-(j-j0)*cos(a));
if(ip>0
&& ip<=m && jp>0
&& jp<=n)
red = r(ip,jp); %
se
il pixel di provenienza sta nel supporto
dell'immagine
green = g(ip,jp); %
prende
il valore dell'immagine
blue = b(ip,jp);
else
red = 0; %
altrimenti
prende il valore nullo (nero)
green = 0;
blue = 0;
end
fprintf(fidw, '%d
%d %d\n', red, green, blue); %
scrive
i valori nel file
end
end
end
Ecco il risultato che si ottiene con angolo=1 radiante

a partire dall'immagine originale dei cammelli
Sapreste deformare l'immagine in modo che l'angolo di rotazione
sia inversamente proporzionale alla distanza del pixel dal centro
dell'immagine di coordinate (i0,j0)? Per questo
basta cambiare la parte in cui si calcolano ip e jp ad esempio
con
a=sqrt((i0-i)^2+(j0-j)^2))/10+0.01;
a=6.28/a;
ip= i0+(i-i0)*cos(a)+(j-j0)*sin(a);
jp=j0+(i-i0)*sin(a)-(j-j0)*cos(a);
il numero 0.01 che è stato aggiunto ad a, serve per evitare
situazioni di singolarità nel centro di rotazione. Ecco il
risultato che si ottiene

Esempio 7. Immagini anamorfiche. Un modo interessante
per applicare deformazioni ad una immagine assegnata consiste nel
fare riflettere l'immagine originale su uno specchio cilindrico o su
una sfera. Ad esempio, supponete di avere uno specchio cilindrico
posto su un piano orizzontale P e considerate un generico raggio che
parte dal vostro occhio, colpisce la superficie del cilindro, viene
riflesso e interseca il piano orizzontale P in un punto p. Lo stesso
raggio se non è riflesso, prosegue oltre il cilindro e
interseca in un punto q un piano obliquo Q posto dietro il cilindro.
Sapreste scrivere le relazioni che legano le coordinate di p e di q?
Se siete in grado di fare questo, potete scrivere un programma che
data un'immagine generica genera una immagine anamorfica che puό
essere "riletta" fisicamente riflettendola in uno specchio
cilindrico.
Esercizi un po piu semplici sono i seguenti:
1-- Simulare come appare una fotografia se viene arrotolata
attorno a un semi cilindro di altezza pari ad una delle due
dimensioni della foto e raggio pari all'altra dimensione diviso per
pigreco. Per questo fare riferimento alla figura seguente
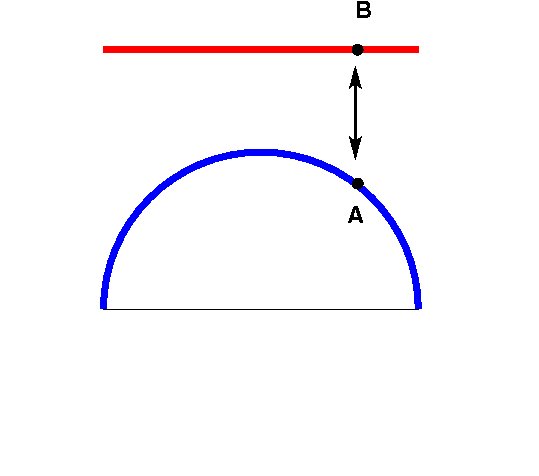
dove, in sezione, la linea blu rappresenta l'immagine originale ed
A un suo generico pixel, mentre la linea rossa rappresenta l'immagine
trasformata e B rappresenta il pixel trasformato di A. Quindi, data
l'immagine blu calcolate la rossa. Un problema analogo consiste nel
calcolare l'immagine blu data la rossa.
2-- Simulare come appare una fotografia se viene posta sotto una
lente di vetro a forma di semi cilindro e vista dall'alto, assumendo
che il vetro abbia un fattore di rifrazione c=1.5, cioe' gli angoli
alfa e beta formati dai raggi incidente e rifratto rispetto al raggio
del cilindro sono tali che sin alfa = c sin beta. Per questo, fare
riferimento alla seguente figura
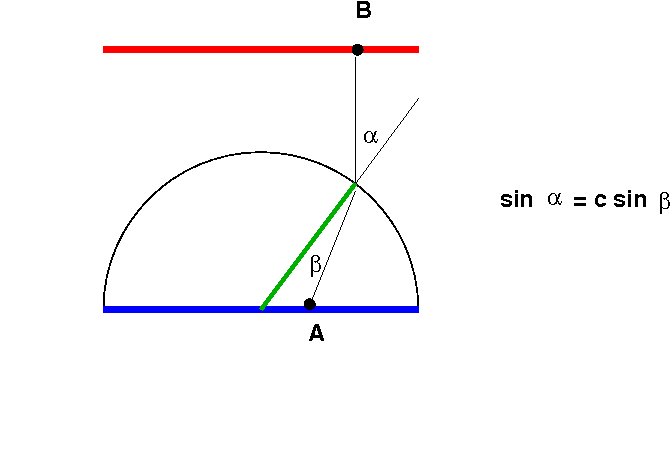
dove, in sezione, la linea blu rappresenta l'immagine originale ed
A un suo generico pixel, mentre la linea rossa rappresenta l'immagine
trasformata e B rappresenta il pixel trasformato di A. In verde e'
tracciato il raggio. Quindi, data l'immagine blu calcolare la rossa.
3-- Simulare come appare una immagine se viene riflessa da un
cilindro lucido nel modo indicato in figura
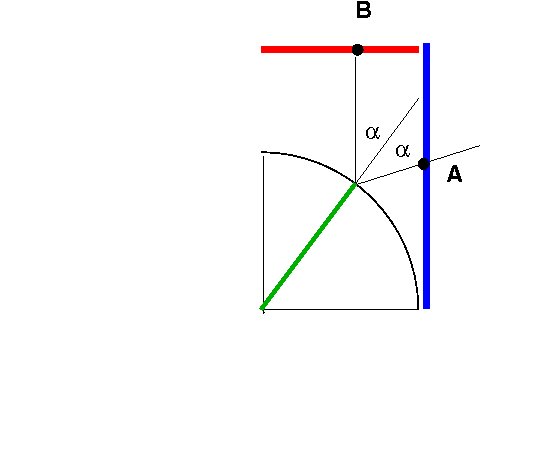
L'immagine e' posta a fianco di un quarto di cilindro con
superficie a specchio e viene vista dall'alto riflessa. I due raggi
incidente e riflesso formano angoli uguali rispetto al raggio del
cilindro.
3.1-Manipolazioni
geometriche con funzioni di variabile complessa.
Interessanti trasformazioni si ottengono utilizzando funzioni di
variabile complessa. Data un'immagine costituita dall'insieme dei
pixel a(i,j), per i=1,...,m, j=1,...,n associamo alla coppia (i,j) un
numero complesso z=z(i,j), ad esempio z=(j-j0)h +
I(i-i0)*h dove abbiamo denotato con I
l'unità immaginaria tale che I2=-1, e dove
abbiamo scelto i0,j0 ed h a nostro piacere.
Oltre all'applicazione (i,j)->z(i,j) consideriamo l'applicazione
"inversa" z(i,j)->(i,j) tale che j è la parte
intera di Re(z)/h +j0, mentre i è la parte intera
di Im(z)/h+i0, dove abbiamo indicato con Re(.) e Im(.) la
parte reale e la parte immaginaria di un numero complesso.
Consideriamo poi una funzione di variabile complessa y=f(z), ad
esempio f(z)=z2/|z|, e costruiamo questa trasformazione
tra coppie di interi (i',j') e (i,j)
(i,j)-> z(i,j), w=f(z),
w->(i',j')
Costruiamo l'immagine che nel pixel di coordinate
(i,j) ha il valore a(i',j') se (i',j') appartiene a [1,m]x[1,n], ha
il valore 0 altrimenti. Come è fatta l'immagine deformata in
questo modo?
Cosa accade con semplici funzioni quali f(z)=zt, se
t è un numero complesso di modulo 1, oppure se t è un
numero reale positivo?
Cosa accade con funzioni più
complesse quali f(z)=z(z/|z|)k, per k intero? Oppure con
f(z)=z-(z3-1)/(2z2)?
Questa e una traccia di programma Octave per deformare immagini
function trasf=complextransform(foto)
%
leggi file
.......
% deforma
k0=round(m/2);j0=round(n/2);
h=2/max(m,n);
trasf=zeros(m,n);
% scandisco supporto della foto
trasformata
for
k=1:m
for
j=1:n
% calcolo numero complesso
corrispondente
z=(j-j0)*h+i*(k-k0)*h;
%
trasformo all'indietro
w=z^2;
%
calcolo le coordinate del pixel corrispondente a
w
kk=round(k0+imag(w)/h);
jj=round(j0+real(w)/h);
%
assegno il colore
if(1<=kk
&& kk<=m && 1<=jj &&
jj<=n)
trasf(k,j)=foto(kk,jj);
else
trasf(k,j)=0;
end
end
end
imshow(trasf,[]);
end
Ecco alcuni esempi




Sapreste simulare l'azione di una lente di ingrandimento
trasformando una immagine in modo da ingrandirne una parte con
continuità e quindi senza strappi lasciando la parte rimanente
inalterata? Le seguenti immagini sono state create da studenti del
corso dell'aa. 2008-2009.



4-Decomposizione spettrale,
filtraggio e compressione.
Ricordiamo che un
vettore v=(v0,...,vn-1) di n
componenti può essere rappresentato nella "base di
Fourier" mediante degli opportuni coefficienti a(i) come
vi=a(0)+a(1) cos(i*2pi/n)+b(1) sin(i*2pi/n)+ a(2)
cos(2i*2pi/n)+b(2) sin(2i*2pi/n)+...+a(m-1) cos((m-1)i*2pi/n)+b(m-1)
sin((m-1)i*2pi/n)+ a(m) cos(mi*2pi/n)
dove si assume n=2m, con m
intero, e pi denota pigreco. I coefficienti a(i) e b(i) possono
essere calcolati, a partire dalle componenti di v, mediante
l'algoritmo FFT (Fast Fourier Transform) della trasformata veloce
discreta di Fourier per il quale esistono numerose implementazioni in
diversi linguaggi di programmazione. La rappresentazione data,
riscritta come
vi=a(0)+A(1) cos(i*2pi/n + B(1))+ A(2)
cos(2i*2pi/n + B(2))+ ...+A(m-1) cos((m-1)i*2pi/n + B(m-1))+A(m)
cos(mi*2pi/n)
permette di interpretare v come una somma di
vettori "oscillanti" con frequenze multiple intere di una
frequenza fondamentale e dotati di varie ampiezze A(i) e fasi B(i).
Questa trasformazione è molto usata dagli ingegneri per
filtrare segnali. Infatti la decomposizione in termini di funzioni
trigonometriche elementari (decomposizione spettrale) ci permette di
conoscere le ampiezze A(i) e le fasi B(i) con cui ogni singola
frequenza elementare compare nel "segnale". Con questa
informazione possiamo fare manipolazioni di segnali molto efficaci,
quali amplificare o ridurre le tonalità acute o gravi di un
suono rappresentato in forma digitale mediante il vettore v. Ad
esempio si può costruire un nuovo vettore w ottenuto
amplificando le componenti in "bassa frequenza" sostituendo
ad esempio i valori A(i) con 2A(i) se i è minore di n/4.
Analogamente possiamo amplificare o attenuare le alte o le medie
frequenze e trasformare il vettore originale in diversi modi. Se il
vettore rappresenta un segnale acustico, ad esempio un brano di
musica, le operazioni descritte hanno l'effetto analogo a quello che
si ottiene regolando i toni in un impianto hifi. Questo tipo di
manipolazione numerica è esattamente quella che svolgono
applicazioni quali "winamp" che riproducono musica digitale
su di un pc.
La relazione tra le componenti del vettore v e i coefficienti a(i)
e b(i) è la seguente: posto u=IDFT(v) il vettore trasformata
discreta inversa di Fourier di v definito da
uj=v0+v1*exp(2j*i*pi/n
)+v2*exp(4j*i*pi/n)+...+vn-1*exp(2j*i*(n-1)*pi/n)
dove i è l'unità immaginaria, allora vale
a(j)=(uj + conj(uj))/2, j=0,1,...,n/2,
b(j)=(uj - conj(uj))/2
dove conj(x) indica il complesso coniugato di x. Per cui il filtro
che possiamo costruire opera nel modo seguente:
dato il segnale v si calcola il suo trasformato u=IDFT(v)
si scalano le componenti di u con un ''filtro'' f=(fj)
cioè si pone w=(wj), wj=uj*fj
si ricostruisce il segnale filtrato come s= DFT(w)
Si può osservare che se v è reale allora il vettore
u è tale che u0 e un/2+1 sono reali
mentre uj è il complesso coniugato di un-j .
Per cui, affinché un filtro f mantenga la realtà del
segnale filtrato s, occorre che f sia ''simmetrico'' nel senso che
fj=fn-j, j=1,...,n/2-1. Basta quindi definire
il filtro in f0,...,fn/2. Un filtro ''passa
alt'' è dato da
fj=1-cos(2*pi*j/n), j=0,...,n/2
infatti, dal grafico della funzione 1-cos(x) si vede che fj
riduce l'ampiezza delle componenti in bassa frequenza, mentre un
filtro passa basso è
fj=1+cos(2*pi*j/n), j=0,...,n/2
Come agisce invece il filtro seguente?
fj=1-cos(3*pi/2 + 2*pi*j/n), j=0,...,n/2
La cosa che a noi interessa fare adesso è applicare queste
decomposizioni spettrali alle righe e alle colonne di una matrice di
pixel relativa ad una immagine digitale in modo da poter amplificare
o ridurre le "componenti in alta frequenza" cioè
andare ad amplificare o a ridurre il dettaglio dei piccoli
particolari. Queste operazioni sono generalmente implementate nei
pacchetti di manipolazione digitale di immagini quali gimp, dove si
preferisce usare al posto della trasformata discreta di Fourier la
trasformata discreta dei coseni. Il nome con cui questa operazione è
conosciuta è "sharpening", cioè rendere più
"incisa" l'immagine. Nel caso bidimensionale di una
immagine mxn, con m ed n pari, il filtro f=(fij) basta
definirlo per i=0,..,m/2, j=0,...,n/2 e poi estenderlo per simmetria
come nel caso monodimensionale.
In Octave il comando u=fft(v) calcola la DFT del vettore v e
ifft(u) calcola la IDFT di u. Nel caso di una matrice A mxn, il
comando fft(A,n,2) calcola la DFT delle n colonne di A, mentre il
comando fft(A,m,1) calcola la DFT delle m righe di A. Per cui
B=fft(fft(A,n,2),m,1) fornisce la DFT bidimensionale (trasformata
delle righe e delle colonne) della matrice A. Analogamente opera la
ifft.
La function che segue mostra come è semplice implementare
l'operazione di filtraggio descritta, una volta che abbiamo a
disposizione un programma che ci calcola la trasformata discreta di
Fourier e la sua inversa.
La function prende in input il nome del file in cui si trova
l'immagine in bianco e nero nel formato pgm, legge l'immagine,
aggiusta le sue dimensioni in modo che siano pari, e poi calcola la
trasformata discreta di Fourier delle righe e delle colonne, effettua
un filtraggio delle componenti in frequenza e ricostruisce l'immagine
filtrata.
function c=filtra(filefoto)
% legge
immagine
fidr=fopen(filefoto,
'r');
ch=fscanf(fidr,
'%s', '1');
n=fscanf(fidr,
'%d', '1');
m=fscanf(fidr,
'%d', '1');
foto=zeros(m,n);
liv=fscanf(fidr,
'%d', '1');
for
i=1:m
for
j=1:n
foto(i,j)=fscanf(fidr,
'%d', '1');
end
end
% ridimensiona a valore
pari
if(mod(m,2)==0)
mm=m;
else
mm=m-1;
end
if(mod(n,2)==0)
nn=n;
else
nn=n-1;
end
a=foto(1:mm,1:nn);
%
costruisce il filtro
filtro=ones(mm,nn);
for
i=1:mm/2+1
for
j=1:nn/2+1
filtro(i,j)=1+(1-cos(pi*2*(i-1)/mm))*(1-cos(pi*2*(j-1)/nn));
end
end
%
completo il filtro per simmetria
filtro(1:mm/2+1,
nn/2+2:nn)=filtro(1:mm/2+1, nn/2:-1:2);
filtro(mm/2+2:mm,
1:nn/2+1)=filtro(mm/2:-1:2, 1:nn/2+1);
filtro(mm/2+2:mm,
nn/2+2:nn)=filtro(mm/2:-1:2, nn/2:-1:2);
% calcolo la
IDFT
ifftfoto=ifft(ifft(a,nn,2),mm,1);
b=ifftfoto
.* filtro;
% calcolo la
DFT
c=fft(fft(b,nn,2),mm,1);
c=real(c);
%
taglio i valori dei pixel tra 0 e 255
c=min(255,max(0,c));
%
mostro l'immagine
imshow(c,[]);
end
Ecco un esempio di immagine ottenuta a
partire dalla fotografia dei cammelli amplificando le alte frequenze.
A sinistra l'immagine filtrata, a destra quella originale. In questo
caso, essendo l'immagine a colori, si è fatto il filtraggio
sulle tre componenti R,G,B. Si puό vedere il maggior dettaglio nei
particolari delle foglie e nei tronchi delle palme.


Cosa si ottiene se si applica un filtro che ''lascia passare''
solo le frequenze medie? Provare con il filtro dato dalla funzione
f(x)=1-cos(x+3*pi/2) calcolata per x=2*pi*j/n.
Si possono ottenere risultati "eccessivi"
con filtraggi strani e fattori di amplificazione che fanno uscire
fuori dal segmento [0,255] molti valori dei pixel dell'immagine
filtrata. Le immagini che seguono sono state ottenute dagli studenti
con valori volutamente anomali del filtraggio o con filtraggi svolti
in modo diverso a seconda del canale del colore.



La stessa tecnica di filtraggio può essere
utilizzata per comprimere un'immagine. Questo avviene memorizzando
solamente i valori delle ampiezze che corrispondono alle frequenze
più basse e si basa sul fatto che generalmente le "alte
frequenze", cioè la ricchezza di dettagli minuscoli, non
sono presenti in tutte le parti di una immagine. Quindi decomponendo
un'immagine in porzioni più piccole ad esempio 8x8 pixel, e
calcolando la rappresentazione spettrale di queste sotto immagini, è
possibile rappresentarle in modo abbastanza fedele memorizzando solo
le basse frequenze nel caso in cui le alte abbiano valori in ampiezza
trascurabili. Questa è l'idea alla base della compressione
JPG.
5-Restauro di immagini
degradate
Fotografie che sono venute sfocate per un diffetto di messa a
fuoco dell'obiettivo possono essere in qualche modo rimesse a fuoco
se si conosce il tipo di sfocatura. Supponiamo di avere scattato una
foto ad una immagine costituita da un solo punto luminoso di
intensità unitaria

con l'obiettivo regolato male si otterrà qualcosa tipo
l'immagine seguente

dove abbiamo volutamente esagerato l'effetto della sfocatura.
Questa nuova immagine sarà definita da dei pixel f(i,j), dove
per comodità facciamo scorrere gli indici i e j da -k a k con
2k+1 l'ampiezza del supporto del puntolino sfocato. La tabella di
numeri f(i,j) descrive quindi il tipo di sfocatura ed è
chiamata in gergo Point-Spread Function, o più semplicemente
PSF. I valori f(i,j) devono sommarsi ad 1 poiché la quantità
di luminosità presente nell'immagine sfocata deve essere
uguale a quella presente nell'immagine originale.
Allora, se
a(i,j) per i=1,m, j=1,n sono i pixel di una immagine originale
costituita da tutti pixel nulli fuorché un solo puntolino di
intensità g in posizione (p,q), l'immagine sfocata b(i,j) avrà
pixel uguali a
b(i,j)=g*f(i-p,j-q), |i-p|, |j-q| <= k
mentre b(i,j)=0 altrove.
L'immagine sfocata di una immagine generica costituita da più
pixel non nulli sarà la somma delle immagini che si ottengono
sfocando i singoli pixel. Vale cioè
b(i,j)=Somma_{p,q} a(p,q)*f(i-p,j-q)
dove la somma è fatta per p=1,m, q=1,n, su tutti gli indici
per cui i-p e j-q sono compresi tra -k e k.
Dal punto di vista
computazionale per sfocare una immagine in bianco e nero basta
calcolare una doppia sommatoria. Per rimettere a fuoco una immagine
basta risolvere un sistema lineare di m*n equazioni in m*n incognite,
ammesso che la matrice del sistema sia non singolare.
Per
immagini a colori la manipolazione va compiuta sui tre canali del
rosso, verde e blu. Per una foto scattata con un macchina fotografica
da 5 megapixel si devono risolvere tre sistemi di 5 milioni di
equazioni e di incognite per poter rimettere a fuoco la foto.
6-Crittografia con le
immagini
Una immagine rappresentata come file pnm è un
nascondiglio efficace per riporre informazioni segrete. Pensate che
una immagine a colori 512x512, come quella dei cammelli, contiene più
di 750.000 byte. Se modifichiamo un solo bit di ciascun pixel abbiamo
la possibilità di nascondere quasi 100.000 byte cioè
quasi centomila caratteri alfanumerici. D'altra parte se aumentiamo o
caliamo di una unità il valore di ciascun pixel
dell'immagine, la tenue variazione di luminosità che otteniamo
su ciascuno dei tre colori non risulta percepibile all'occhio umano.
Per cui la foto che si ottiene modificandoi i valori numerici in
questo modo appare dal punto visivo identica all'immagine
originale.
Nelle immagini che seguono sono stati modificati rispettivamente
1,2,3,4,5,6 bit di ciascun pixel. L'informazione che abbiamo nascosto
nell'immagine è quella di parte dell'iimmagine originale
stessa, costituita dai valori numerici dei pixel di parte
dell'immagine originale dei cammelli.





Si osservi che nelle prime tre immagini non si apprezzano
particolari variazioni.
L'istruzione che sostituisce i k
bit meno significativi del byte pixel
con l'intero h (formato da
al più k bit) è la seguente
pixel=pixel-mod(pixel,2**k)+h
Infatti l'istruzione mod(pixel,2**k) fornisce il valore di pixel
modulo 2k cioè il numero intero formato
dai k bit meno significativi di pixel.
Per decodificare
l'informazione occorre estrarre l'intero formato dai k bit meno
significativi di ciascun pixel. Per cui l'istruzione che si usa è
info=mod(pixel,2**k)
I
vari pezzettini di informazione andranno poi "incollati" in
un singolo byte per recuperare la lettera corrispondente al byte.
Questo compito è lasciato per esercizio.
Per completare il
programma che cripta e decodifica sono utili due funzioni: la prima,
dato un carattere alfanumerico fornisce il byte con cui viene
identificato (codice ASCII); la seconda, dato il codice fornisce il
carattere alfanumerico corrispondente.








































