16^a46 Si cylindrus scalenus plano secetur per axem ad rectos angulos basi, et rursum plano secundo ad primum recto ita ut planorum communis sectio faciat⁴⁷ angulos cum parallelogrammi per axem lateribus aequales ipsius parallelogrammi angulis sed subcontrarie positos: sectio secundi plani in cylindro circulus est, vocaturque subcontraria sectio.

Sit cylindrus scalenus, cuius axis ab et bases ipsi ef cd circuli circum centra a b qui sectus plano per axem ad bases recto faciat parallelogrammum cdfe. Moxquoque secetur plano grh recto ad ipsum parallelogrammum cf ita ut recta gh communis sectio planorum faciat angulum ghd aequalem angulo cdf.

Aio quod sectio

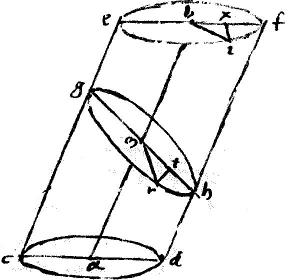
grh quam planum grh facit in cylindro, circulus est: capiatur enim in periferia grh punctum quodvis ut puta r a quo ducatur ad diametrum gh perpendicularis rt et connectatur mr. Cumque anguli ghd cdh sint per hypothesim aequales et ipsae ec df paralleli, atque ideo ipsae gh cd ef sint aequales, et eorum dimidia mh bf aequalia; propterea abscisa de bf ipsa bx aequali ipsi mt supererit xf aequalis ipsi th. Quare, sicut bx ad xf sic mt ad th. Ergo per praecedentem 14^am48 ipsae xi tr aequales. Itaque connexa bi cum anguli ad x t sint recti, erunt, per 4^am primi, ipsae mr bi aequales, sed bi aequalis ipsi bf per diffinitionem circuli; et bf⁴⁹ aequalis ipsi mh ergo mr aequalis ipsi mh.

Non aliter ostendam quod omnis recta quae a periferia grh ad punctum m aequalis erit ipsi mh. Quam ob rem universae rectae a puncto m ad periferiam grh sunt ad invicem aequales: itaque per conversionem diffinitionis circuli periferia grh circulus erit; quod fuit propositum.

Appellatur autem sectio subcontraria, quando non parallelus est cylindri basibus, sed ad eosdem circulos subcontrarie posita.⁵⁰

3 Idem aliter⁵¹ ostendam. Ducatur a quolibet puncto periferiae grh ut puta a puncto r ad diametrum gh recta perpendicularis rt quae secabit⁵² diametrum gh per 12^am huius et per punctum t agatur diametro cd parallelus kl et producatur planum, in quo iacent kl rt parallelum circulo cd per 15^am 11ⁱ eritque per 13^am huius, sectio krl⁵³ circulus: 4 et per diffinitionem plani ad planum recti, rt perpendicularis erit ad parallelogrammum cf et ideo ipsi diametro kl⁵⁴ perpendicularis. 5 Et quoniam per hypothesim angulus ghd aequalis est angulo cdh et ideo angulo klf ob id anguli lh anguli tlh sunt equales et ideo

per 6^am primi latera tl th aequalia; nec alia ratione trianguli gtk latera gt tk aequalia: sed per 8^am 6ⁱ rectangulum kt tl aequum est quadrato tr. Ergo rectangulum gt th aequum quadrato tr. Similiter ostendam⁵⁵ quod omnis rectae a flexa grh perpendicularis in rectam gh quadratum aequum erit ei rectangulo, quod sub segmentis ipsius gh. Quare per praemissam grh semicirculus est; non aliter ostendam quod flexa gsh semicirculus est et ideo tota flexa grhs circulus est, quod est propositum. Et haec est demonstratio Sereni.