SERENI CILINDRICORUM LIBER SECUNDUS

<PROPOSITIONES>

1^a Conica ellipsis et cylindrica, quarum diametri maiores sunt minoribus proportionales: sunt invicem similes.

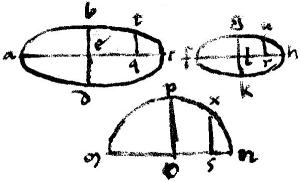
Sit conica ellipsis abcd cuius diametri ac bd centrumque e. Item cylindrica ellipsis fghk cuius diametri fh gk centrumque l. Sitque sicut diameter ac ad diametrum fh sic diameter bd ad diametrum gk.

Aio quod similes sunt ellipses abc fgh.

Exponatur enim ad libitum recta mn super¹ quam in puncto o bifariam secta describatur semicirculus mpn et ducatur ipsi mn perpendicularis semidiameter op.

Mox secentur diametri q r s ad eandem rationem in punctis q r s et excitentur diametris perpendiculares usque ad periferias rectae qt ru sx. Eritque per 61^am et 64^am primi Conicorum, sicut be ad po sic tq ad xs et permutatim, sicut be ad tq sic po ad xs. Sed per 17^am vel 18^am praemissi libelli, sicut po ad xs sic gl ad ur. Ergo sicut be ad tq sic gl ad ur². Idem ostendam quotiescumque sectis ad eandem rationem diametris ac fh³. Quare per diffinitionem similium sectionum similes sunt sectionis abc fgh; quod est propositum.

Vel sic per additionem post 59^am in primo Conicorum elementorum vel additionem post 64^am, sicut quadratum ae ad rectangulum aq qc sic quadratum be ad quadratum tq et per 21^am praecedentis libelli, sicut quadratum fl ad rectangulum fr rh sic quadratum gl ad quadratum ur. Sed quadratum ae ad rectangulum aq qc sicut quadratum fl ad rectangulum fr rh quoniam scilicet tales rationes componuntur ex rationibus laterum per 24^am 6ⁱ Euclidis et laterum rationes sunt caedem propter proportionalem sectionem; diametrorum⁴ ac fh. Igitur, per 11^am quinti⁵, sicut quadratum be ad quadratum tq sic quadratum gl ad quadratum ur. Quare et sicut be ad tq sic gl ad ur idem sequitur quotiescumque sectis ac fh diametris ad eandem rationem⁶. Suntque diametri ac fh diametris bd gk proportionales. Itaque rursum per diffinitionem similium sectionum similes sunt sectiones abc fgh conica et cylindrica quod erat demonstrandum.