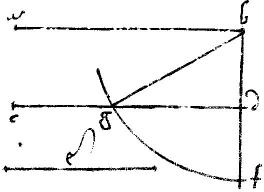
28a Propositis duobus cylindris altero secto ellipsi: reliquum plano secundario sic secare ut similem faciat ellipsim.
Sunto duo cylindri pqsr cuius axis no bases rs pq parallelogrammum quod per axem basi rectum pqsr ellipsis t![]() uy cuius prima diameter tu secunda
uy cuius prima diameter tu secunda ![]() y centrum z in axe on. Item cylindrus cdfe cuius axis ab bases cd ef parallelogrammum, quod per axem basi rectum cdfe.
y centrum z in axe on. Item cylindrus cdfe cuius axis ab bases cd ef parallelogrammum, quod per axem basi rectum cdfe.
Oportet ipsum cf cylindrum plano secundario sic secare, ut sectio sit ellipsis ipsi tu ellipsi similis.
Sicut est minor99 diametrorum ellipseos t![]() u ad maiorem sic sit diameter cd ad rectam
u ad maiorem sic sit diameter cd ad rectam ![]() eritque linea
eritque linea ![]() maior quam cd. Itaque per praecedentem interponatur ipsis parallelis ce df ipsi
maior quam cd. Itaque per praecedentem interponatur ipsis parallelis ce df ipsi ![]() rectae aequalis recta gh super100 quam erigatur ipsi cf parallelogrammo rectum planum secundarium faciens in cylindro sectionem gkhl cuius prima diameter gh secunda kl centrumque m101 eritque102 talis sectio per diffinitionem ellipsis.
rectae aequalis recta gh super100 quam erigatur ipsi cf parallelogrammo rectum planum secundarium faciens in cylindro sectionem gkhl cuius prima diameter gh secunda kl centrumque m101 eritque102 talis sectio per diffinitionem ellipsis.
Aio itaque quod simili est ellipsis gkh ellipsi t![]() u.
u.
Cum enim ellipseos t![]() u minor diameter ad maiorem sit, sicut ellipseos gkh minor diameter quae est cd per corollarium 14ae, ad maiorem gh erunt per 23am huius, ellipses gkh t
u minor diameter ad maiorem sit, sicut ellipseos gkh minor diameter quae est cd per corollarium 14ae, ad maiorem gh erunt per 23am huius, ellipses gkh t![]() u similes. Itaque cylindrum cf secuimus plano secundario faciente ellipsim gkh similem ellipsi t
u similes. Itaque cylindrum cf secuimus plano secundario faciente ellipsim gkh similem ellipsi t![]() u datae in cylindro ps quod faciendum proponitur.
u datae in cylindro ps quod faciendum proponitur.
Scholium
Attendendum quod hac via prima diameter gh semper erit longior quam kl secunda qualiscumque fuerit cylindrus cf.
Verum si scalenus fuerit cylindrus cf tunc continget interdum primam diametrum gh minorem esse secunda hoc pacto.
Sicut est maior diametrorum ellipseos t![]() u ad minorem, sic sit diameter cd ad lineam
u ad minorem, sic sit diameter cd ad lineam ![]() quae si non fuerit minor brevissima linea cadente inter parallelos ce df poterit per premissam, ei aequalis interponi dictis parallelis; quae sit gh fiatque sectio gkh modo praedicto; eritque prima eius103 diameter gh minor quam secunda cd vel kl. Quod si linea
quae si non fuerit minor brevissima linea cadente inter parallelos ce df poterit per premissam, ei aequalis interponi dictis parallelis; quae sit gh fiatque sectio gkh modo praedicto; eritque prima eius103 diameter gh minor quam secunda cd vel kl. Quod si linea ![]() fuerit minor brevissima linea cadente inter parallelos ce df unde non erit ideo possibile.
fuerit minor brevissima linea cadente inter parallelos ce df unde non erit ideo possibile.
Corollarium
Manifestum est ergo quod cylindricae sectiones, quarum primae diametri proportionales sunt basibus parallelogrammorum primariorum104, sunt similes.
Nam per corollarium 14ae tales parallelogrammorum bases sunt secundis sectionum diametris aequales: quare per 23am patet corollarii veritas105.