5^a Proposito cono, sectoque ellipsi ad libitum: super eandem basim ad eandem altitudinem cylindrum constituere, qui sectus eodem, quo conus, plano ellipsim¹⁸ faciat similem ellipsi conicae.

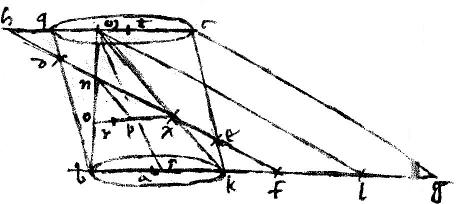
Sit conus bmk cuius basis bk eiusque centrum a qui sectus primario triangulo bmk secetur item secundario plano faciente ellipsim, cuius prima diameter sit n.

Oportet itaque super basim bk et sub fastigio verticis m cylindrum statuere, qui sectus plano faciente ellipsim, cuius diameter n faciat ellipsim similem.

Producatur diameter n donec occurrat diametro bk ad signum f et adhuc ulterius producatur, et compleatur parallelogrammum fhml et per 9^am 6ⁱ ipsis kl lb intersit media proportionalis kg et producta hm compleatur parallelogrammum lmcg item compleatur¹⁹ parallelogrammum bkcq cuius latera²⁰ bq kc secent ipsum hf in punctis d e et secta cq bifariam in puncto t describatur super centrum t ad spacium tc circulus in plano quod sit parallelum circulo²¹ bk et circumductis semidiametris²² tc ak usque²³ quaque parallelis ac rectam ck circumducentibus, formetur²⁴ cylindrus, qui sectus ipso plano ellipseos n faciet ellipsim, cuius prima diameter erit de per diffinitionem.

Aio itaque quod ellipsis cylindrica²⁵ cuius prima diameter de similis est ellipsi conicae, cuius prima diameter n quod sic ostendo.

Sit ipsi bg parallelus o et np parallelus ipsi mk et occurrens ipsi o apud p. Item inter p o medii proportianalis sit r eritque per 71^am primi Conicorum r secunda diametros ellipsis, cuius prima diameter n.

Adhuc a puncto m cadat ipsis ck qb parallelus ms eritque propter aequalitatem triangulorum msl ckg latus sl aequale lateri kg.

Quare cum lk kg lb sint continue proportionales erunt et lk sl lb continue proportionales.

Cumque sint p r o continue proportionales et propter triangulorum bml on similitudinem, itemque triangulorum kml pn similitudinem ex aequidistantia linearum p ad lk sicut o ad lb et permutatim p ad o sicut lk ad lb.

Quare per conversionem aequae proportionis, sicut lk ad sl sic p ad r et permutatim, sicut lk ad p sic sl ad r.

Sed lk ad p sicut lm ad n ob dictam triangulorum similitudinem ergo sicut lm ad n sic sl ad r et permutatim sicut lm ad sl sic n ad r.

Sed sicut lm ad sl sic fd ad bf propter triangulorum sml bdf similitudinem. Et ideo per 2^am 6ⁱ²⁶ sicut de ad bk.

Igitur sicut de ad bk sic n ad r.

Verum de bk per corollarium 14^ae praemissi, sunt diametri cylindricae sectionis de ipsae autem n r iam fuerunt diametri conicae ellipseos n.

Ergo proportionales sunt ellipseos de diametri diametris ellipseos n.

Quare per primam huius, cylindrica ellipsis de similis est conicae²⁷ ellipsi n.

Itaque super basim bk coni bmk sub ipsius coni fastigio ereximus²⁸ cylindrum bc qui sectus plano secundario, quo conus, bmk facit ellipsim de similem conicae ellipsi n quod faciendum proponitur.